1. Frage: Die Lösung ist 4 x 6 x 5 = 120.
Die Zahl 120 ist mathematisch gesehen weniger wichtig als das Produkt der drei Zahlen 4, 6 und 5. Falls nicht klar sein sollte, wieso man die drei Zahlen multiplizieren muss, hier eine Erklärung: für das Überqueren des ersten Flusses gibt es 4 Möglichkeiten. Für jede dieser 4 Möglichkeiten hat man jeweils 6 Möglichkeiten, den 2. Fluss zu überqueren. Das erklärt, weshalb es 24 Möglichkeiten gibt, die ersten beiden Flüsse zu überqueren. Und nun hat man für jede der bisher 24 Möglichkeiten noch deren fünf, den 3. Fluss zu überqueren.
 
2. Frage: Die Lösung ist 90 x 89 x 88.
Für die erste Zahl hat man 90 Möglichkeiten. Dann ist eine Zahl bereits verwendet worden, man hat also noch deren 89. Je nachdem, welche Zahl in der ersten Ziehung gezogen wurde, gibt es für die zweite Ziehung andere Möglichkeiten. Entscheidend ist aber, dass die Anzahl der Möglichkeiten für die zweite Ziehung nicht ändert. Für die dritte Zahl hat man genau 88 Möglichkeiten, egal welche zwei Zahlen vorher gezogen wurden.

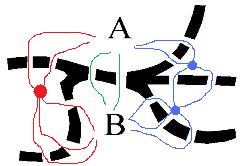
Die Lösung beträgt 20 = 2 x 3 + 2 + 2 x 2 x 3

Man hat eigentlich drei Möglichkeiten, nämlich links über den roten Punkt, direkt (grüne Wege) oder rechts über die blauen Punkte. Für die roten Wege gibt es nach der Produktregel 6 = 2 x 3 Möglichkeiten. Direkte Wege gibt es deren 2 und über die blauen Punkte hat man 12 Möglichkeiten. Diese drei Zahlen muss man nun addieren, denn man fährt entweder über den roten Punkt oder direkt oder über die blauen Punkte.

Das sprachliche "sowohl ... als auch" führt also mathematisch zu einem Produkt, das sprachliche "entweder ... oder" führt auf eine Summe.
Manche Leute haben Schwierigkeiten, das sprachliche "und" kombinatorisch richtig zu deuten. (Für die roten Wege fährt man von A zum roten Punkt und dann vom roten Punkt weiter nach B.) Hier stellt uns die deutsche Sprache eine Falle, denn das "und" bedeutet "... und gleichzeitig ... " und führt somit bei der Berechnung zu einem Produkt.

Lösungen und Kommentare finden sich im pdf-Dokument.

Lösungen und Kommentare finden sich im pdf-Dokument.

Man hat 10 x 8 x 12 Möglichkeiten, ein Gremium zu bilden, in welchem kein Vertreter Italiens Einsitz nimmt.
Ebenso hat man 10 x 8 x 6 Möglichkeiten für ein Gremium ohne Briten, 10 x 12 x 6 Möglichkeiten ohne Franzosen und 8 x 12 x 6 ohne Deutsche.
Diese vier Zahlen sind zu addieren, denn es fehlt entweder Italien oder Grossbritannien oder Frankreich oder Deutschland.
Das ergibt 10 x 8 x 12 + 10 x 8 x 6 + 10 x 12 x 6 + 8 x 12 x 6 = 2736. Die letzte Zahl ist aus mathematischer Sicht unwichtig. Der Lösungsweg ist viel entscheidender.